 入門
入門 入門
入門
![]()


TeX はスタンフォード大学のクヌース教授が自分自身の著書をコンピュータを使って作成するために作られた組版システム(印刷ソフト)です。始めは UNIX などの大型コンピュータでしか使えませんでしたが,1980年代後半からPC-9800シリーズなどのパソコンで使えるものが登場し,現在では Windows95, Macintoshなど,ほとんどのパソコンで使用可能です。特徴としては次のようなものがあげられます。
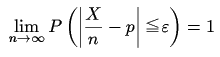
などの複雑な式もかける。
…文字を{\Large 大きく}するためには…
と書きます。
これに対し多くの皆さんが使っているワープロは画面で見たままのイメージが出力されるWYSIWYG方式(What You See Is What You Get)と呼ばれます。
そのため始めのうちは慣れない人にとっては少し使いにくいかもしれません。しかし,ワープロのぎこちない数式と違う美しい数式は少々の使いにくさを乗り越えようと思わせるほどの魅力を持っています。大学の理工系の学部では TeX を使っているところが増えているので先生方の中にも既に TeX を使ったことがあるという方もいるかもしれません。また,BASIC などのプログラミングの心得のある方ならそれほど障害はないはずです。
つまり,ワープロがインタプリタ型であるのに対し,TeX はコンパイラ型の文書作成システムです。数式を含んだような複雑な文書ではワープロのようなインタプリタ型のシステムでは表示に時間がかかってしまいます。そこで TeX ではあらかじめ文書とともにコマンドを埋め込んだソースファイルをコンパイルすることで高速な表示を可能にしています。(プログラムをしたことがある人にしかわからない文章になってしまった。(^^;
しかし,インストールするにはある程度の知識が必要なので全くの初心者には難しいと思います。そこで,初心者の方はインストールが簡単にできる次の書籍を購入することをお勧めします。現在(2000年12月)買うなら Vol.1 Basic Kit 1999 が良いでしょう。
TeX はスタイルファイルと呼ばれるレイアウトを扱うファイルが充実するほど使い勝手が良くなりますし,強力なマクロを備えていますので報告書などの形式の決まった書類ならば,著者や本文・タイトルなどを入力するだけで適切な位置に適切な大きさで,番号などは自動的に振りながらという具合に,レイアウトはコンピュータのほうが自動的に決めてくれます。
私自身が数学を教えていますので個人的趣味と必要性に迫られて,現在普通高校で行われている県下一斉模試の数学用のスタイルファイルと数学の中間・期末試験用のスタイルファイルを作成しています。
クリックすれば(Netscape Navigator の場合は「Shift」を押しながらクリックするとダウンロード出来るようです)ディスクへの保存を促すダイアログが開かれると思います(セキュリティに関するダイアログが開かれる場合もあるかもしれません)。PACK for WIN などにも収録されているのでお持ちの方は CD-ROM を検索してみて下さい。http://www.vector.co.jp/ にも収録されているので,商用ネットワークから接続している方はそちらをご利用下さい。
ただし,若干の知識が必要となりますので,すぐにはうまく行かないかもしれません。その場合はメール下さい。
以下に数学の試験問題のサンプル(少し分かり易く変更しているのと他のファイルが必要なため,このままではコンパイル出来ません)と出力結果を載せておきます。
\documentstyle[11pt,b5j,ascmac,jtwocolumn,b4tate]{jarticle}
\begin{document} % 本文の始まり
\twocolumn[
\hskip6zw {\Large 数学学年末考査} % \hskipは水平方向にスペースを作ります
\hskip1zw H7.2.28 \hfill
\underline{1年 \hskip2zw 組 \hskip2zw 号 \hskip3zw 氏名 \hskip30ex}
\vspace*{2ex}
\mbox{} ]
\toi
次の \raisebox{0mm}{\fbox{\rule[1mm]{0mm}{2mm}\hskip7mm}} を埋めよ。
\subtoi 初項が \(2a\) ,公差が $-5$ の等差数列の
一般項 \(a_n=\sikaku{10}\) で
,$n$項までの和 \(S_n=\sikaku{20}\) である。
\subtoi 初項が3,公比が \({\,1\, \over 2}\) の等比数列の
一般項は \(a_n=\sikaku{10}\) で, $n$ 項までの
和は \(S_n=\sikaku{20}\) である。
\subtoi \(2+3+4+\cdots 10\) を $\sum$ を用いて表すと \sikaku{20}
\subtoi \( \sum^n_{k=1}(2k+3) \) の和は \sikaku{20}
\subtoi \( \sum^n_{k=1}5\cdot 2^{k-1} \) の和は \sikaku{20}
\subtoi \( \sum^n_{k=1}{1 \over k(k+1)} \) の和は \sikaku{20}
\subtoi 第10項が230,第25項が $-220$ の等差数列がある。
初項は \sikaku{10} ,公差は \sikaku{10} ,なので
第 \sikaku{10} 項が170となる。
また,初項から第 \sikaku{10} までの和が最大で,
そのときの値は \sikaku{10} となる
\subtoi 第3項が $-12$ ,第6項が96の等比数列がある。\\
初項は \sikaku{10} ,公比は \sikaku{10} である。したがって
初項から第 \sikaku{10} 項までの和をとれば63となる。
\subtoi 2と20の間に \sikaku{10} 個の数を入れて,全体が等差数列となるように
し,この等差数列の総和が143となるようにするには公差を \sikaku{10} と
すればよい。
\toi
次の数列の初項から第 $n$ 項までの和を求めよ。
\qquad \(1\cdot3,~2\cdot4,~3\cdot5,~4\cdot6,\cdots \)
\newpage
\toi
数列 \(2,~2+4,~2+4+6,~2+4+6+8,\cdots\cdots \) \\
について,次の問いに答えよ。
\subtoi 第 $n$ 項を $n$ の式で表せ。
\vfill
\subtoi 初項から第$n$項までの和を求めよ。
\vfill
\vfill
\vfill
\toi
次の数列の和を求めよ。
\subtoi \(1+2\cdot2+3\cdot2^2+4\cdot2^3+
\cdots\cdots +n\cdot2^{n-1}\)
\vfill
\vfill
\vfill
\vfill
\vfill
\vfill
\subtoi \(1\cdot(2n-1)+3\cdot(2n-3)+5\cdot(2n-5)+
\cdots\cdots +(2n-1)\cdot1\)
\vfill
\vfill
\vfill
\vfill
\vfill
\vfill
こういったソースファイルを TeX でコンパイルすることで次のような試験問題ができあがります。

あなたも TeX をはじめてみませんか?。(結構苦労すると思うけど……)